已知函数f+k(其中A>0.ω>0.0≤φ≤π)是R上的偶函数.且f(x)还满足以下三个条件:①最大值是3,②图象关于点对称,③在区间[0.π]上是单调函数.则函数f(x)的表达式是 .
已知函数f(x)=Asin(ωx+φ)+k(其中A>0,ω>0,0≤φ≤π)是R上的偶函数,且f(x)还满足以下三个条件:
①最大值是3;②图象关于点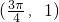 对称;③在区间[0,π]上是单调函数.则函数f(x)的表达式是________.在线课程
对称;③在区间[0,π]上是单调函数.则函数f(x)的表达式是________.在线课程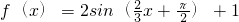
分析:由函数的对称中心的纵坐标求出k的值,由最值求出A,根据函数f(x)是R上的偶函数,0≤φ≤π 可得 φ 值,由 sin(ω•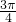 +
+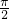 )=0,可得ω的值.
)=0,可得ω的值.
解答:由①函数的最大值是3、②图象关于点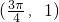 对称,可得 k=1,A+1=2,故A=2,故函数f(x)=2sin(ωx+φ)+1.
对称,可得 k=1,A+1=2,故A=2,故函数f(x)=2sin(ωx+φ)+1.
根据函数f(x)是R上的偶函数,0≤φ≤π 可得 φ=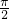 . 再由 sin(ω•
. 再由 sin(ω•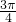 +
+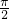 )=0,ω>0,可得ω•
)=0,ω>0,可得ω•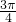 +
+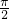 =π,ω=
=π,ω=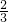 .
.
经检验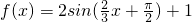 满足③在区间[0,π]上是单调函数,
满足③在区间[0,π]上是单调函数,
故答案为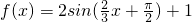 .
.
点评:本题主要考查利用y=Asin(ωx+φ )的图象特征,由函数y=Asin(ωx+φ )的部分图象求解析式,属于中档题.

①最大值是3;②图象关于点
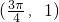 对称;③在区间[0,π]上是单调函数.则函数f(x)的表达式是________.在线课程
对称;③在区间[0,π]上是单调函数.则函数f(x)的表达式是________.在线课程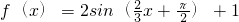
分析:由函数的对称中心的纵坐标求出k的值,由最值求出A,根据函数f(x)是R上的偶函数,0≤φ≤π 可得 φ 值,由 sin(ω•
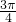 +
+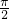 )=0,可得ω的值.
)=0,可得ω的值.解答:由①函数的最大值是3、②图象关于点
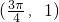 对称,可得 k=1,A+1=2,故A=2,故函数f(x)=2sin(ωx+φ)+1.
对称,可得 k=1,A+1=2,故A=2,故函数f(x)=2sin(ωx+φ)+1.根据函数f(x)是R上的偶函数,0≤φ≤π 可得 φ=
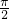 . 再由 sin(ω•
. 再由 sin(ω•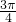 +
+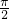 )=0,ω>0,可得ω•
)=0,ω>0,可得ω•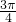 +
+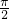 =π,ω=
=π,ω=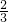 .
.经检验
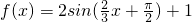 满足③在区间[0,π]上是单调函数,
满足③在区间[0,π]上是单调函数,故答案为
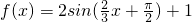 .
.点评:本题主要考查利用y=Asin(ωx+φ )的图象特征,由函数y=Asin(ωx+φ )的部分图象求解析式,属于中档题.



