在△ABC中.a.b.c分别是角A.B.C的对边.向量=.=.且∥.(1)求角A的大小,(2)若.sin(B-C)=cosA.求边长b和c.
在△ABC中,a,b,c分别是角A,B,C的对边,向量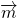 =(2cos2A+3,2),
=(2cos2A+3,2),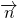 =(2cosA,1),且
=(2cosA,1),且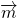 ∥
∥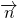 .
.
(1)求角A的大小;
(2)若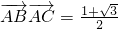 ,sin(B-C)=cosA,求边长b和c.在线课程解:(1)∵向量
,sin(B-C)=cosA,求边长b和c.在线课程解:(1)∵向量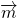 =(2cos2A+3,2)
=(2cos2A+3,2)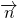 =(2cosA,1),且
=(2cosA,1),且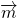 ∥
∥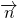 ,∴(2cos2A+3)×1-(2cosA)×2=0,解得 cosA=
,∴(2cos2A+3)×1-(2cosA)×2=0,解得 cosA= ,
,
在△ABC中,可得A=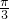 .
.
(2)∵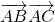 =
= bc•sinA=
bc•sinA=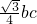 =
=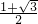 ,
,
∴bc=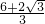 ①.
①.
∵sin(B-C)=cosA= ,
,
∴B-C=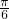 或 B-C=
或 B-C=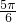 (舍去).
(舍去).
再由 B+C=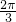 ,可得 B=
,可得 B=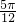 ,C=
,C=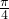 .
.
再由正弦定理可得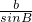 =
=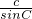 ,
,
∴ =
=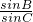 =
=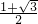 ②.
②.
由①②解得 b=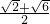 ,c=
,c=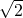 .
.
分析:(1)利用两个向量共线的性质可得(2cos2A+3)×1-(2cosA)×2=0,解得 cosA= ,从而求得角A的大小.
,从而求得角A的大小.
(2)由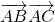 =
=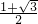 可得 bc=
可得 bc=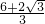 ①,再由sin(B-C)=cosA=
①,再由sin(B-C)=cosA= ,可得B-C的值,根据B+C=
,可得B-C的值,根据B+C=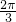 ,求出B、C的值.利用正弦定理求出
,求出B、C的值.利用正弦定理求出  =
=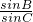 =
=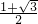 ②,结合①②解得边长b和c.
②,结合①②解得边长b和c.
点评:本题主要考查两个向量共线的性质,两个向量的数量积的定义,正弦定理的应用,属于中档题.

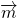 =(2cos2A+3,2),
=(2cos2A+3,2),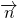 =(2cosA,1),且
=(2cosA,1),且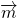 ∥
∥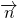 .
.(1)求角A的大小;
(2)若
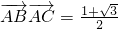 ,sin(B-C)=cosA,求边长b和c.在线课程解:(1)∵向量
,sin(B-C)=cosA,求边长b和c.在线课程解:(1)∵向量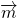 =(2cos2A+3,2)
=(2cos2A+3,2)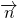 =(2cosA,1),且
=(2cosA,1),且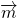 ∥
∥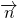 ,∴(2cos2A+3)×1-(2cosA)×2=0,解得 cosA=
,∴(2cos2A+3)×1-(2cosA)×2=0,解得 cosA= ,
,在△ABC中,可得A=
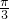 .
.(2)∵
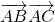 =
= bc•sinA=
bc•sinA=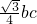 =
=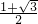 ,
,∴bc=
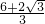 ①.
①.∵sin(B-C)=cosA=
 ,
,∴B-C=
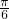 或 B-C=
或 B-C=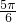 (舍去).
(舍去).再由 B+C=
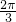 ,可得 B=
,可得 B=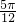 ,C=
,C=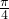 .
.再由正弦定理可得
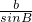 =
=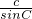 ,
,∴
 =
=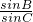 =
=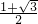 ②.
②.由①②解得 b=
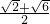 ,c=
,c=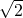 .
.分析:(1)利用两个向量共线的性质可得(2cos2A+3)×1-(2cosA)×2=0,解得 cosA=
 ,从而求得角A的大小.
,从而求得角A的大小.(2)由
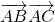 =
=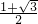 可得 bc=
可得 bc=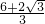 ①,再由sin(B-C)=cosA=
①,再由sin(B-C)=cosA= ,可得B-C的值,根据B+C=
,可得B-C的值,根据B+C=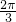 ,求出B、C的值.利用正弦定理求出
,求出B、C的值.利用正弦定理求出  =
=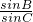 =
=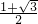 ②,结合①②解得边长b和c.
②,结合①②解得边长b和c.点评:本题主要考查两个向量共线的性质,两个向量的数量积的定义,正弦定理的应用,属于中档题.



