给出下列四个命题:①“?x∈R.x2-x＞0 的否定是“?x∈R.x2-x≤0 ,②对于任意实数x.有f.且x＞0时.f′＞0.则x＜0时.f′,③函数是偶函数,④若对?x∈R.函数f.则4是该函数的
给出下列四个命题：
①“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x≤0”；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x），且x＞0时，f′（x）＞0，g′（x）＞0，
则x＜0时，f′（x）＞g′（x）；
③函数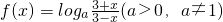
是偶函数；
④若对?x∈R，函数f（x）满足f（x+2）=-f（x），则4是该函数的一个周期，其中真命题的个数为
A.1B.2C.3D.4在线课程C
分析：由题意，依次分析可得，①符合特称命题的否定形式，正确；②不能判断其单调性，错误；③将（-x）代入f（x）中，分析可得，f（-x）=f（x），则f（x）是偶函数，正确；④根据题意，f（x+4）=-f（x+2）=f（x），则4是该函数的一个周期，正确；进而可得答案．
解答：由题意，依次分析可得，
①、符合特称命题的否定形式，正确；
②、根据题意，f（x）是奇函数，g（x）是偶函数；又由奇函数在定义域内单调性相同，偶函数单调性相反，所以x＜0时，f′（x）＞0，g′（x）＜0，所以f′（x）＞g′（x），故正确；
③、根据题意，f（-x）=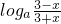
=-
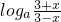=-f（x），则f（x）是奇函数，错误；
④、根据题意，f（x+4）=-f（x+2）=f（x），则4是该函数的一个周期，正确；
综合可得，有3个命题正确，
故选C．
点评：本题考查命题真假的判断，涉及特称命题的否定、函数的周期性、单调性的判断等知识点，综合性很强，需要认真分析．
①“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x≤0”；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x），且x＞0时，f′（x）＞0，g′（x）＞0，
则x＜0时，f′（x）＞g′（x）；
③函数
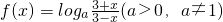是偶函数；④若对?x∈R，函数f（x）满足f（x+2）=-f（x），则4是该函数的一个周期，其中真命题的个数为
A.1B.2C.3D.4在线课程C
分析：由题意，依次分析可得，①符合特称命题的否定形式，正确；②不能判断其单调性，错误；③将（-x）代入f（x）中，分析可得，f（-x）=f（x），则f（x）是偶函数，正确；④根据题意，f（x+4）=-f（x+2）=f（x），则4是该函数的一个周期，正确；进而可得答案．
解答：由题意，依次分析可得，
①、符合特称命题的否定形式，正确；
②、根据题意，f（x）是奇函数，g（x）是偶函数；又由奇函数在定义域内单调性相同，偶函数单调性相反，所以x＜0时，f′（x）＞0，g′（x）＜0，所以f′（x）＞g′（x），故正确；
③、根据题意，f（-x）=
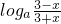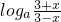=-=-f（x），则f（x）是奇函数，错误；④、根据题意，f（x+4）=-f（x+2）=f（x），则4是该函数的一个周期，正确；
综合可得，有3个命题正确，
故选C．
点评：本题考查命题真假的判断，涉及特称命题的否定、函数的周期性、单调性的判断等知识点，综合性很强，需要认真分析．
