已知圆C的圆心在x轴上.曲线x2=2y在点A(2.2)处的切线l恰与圆C在A点处相切.则圆C的方程为 .
已知圆C的圆心在x轴上,曲线x2=2y在点A(2,2)处的切线l恰与圆C在A点处相切,则圆C的方程为________.在线课程(x-6)2+y2=20
分析:先对函数进行求导,根据导函数在点A处的值为切线的斜率可得切线方程,再利用直线与圆相切求出圆心坐标及、半径即可得出答案.
解答:∵y= x2∴y'=x
x2∴y'=x
当x=2时,y'=2,
∴点A(2,2)处的切线方程为:y-2=2(x-2)即:2x-y-2=0
∵切线l恰与圆C在A点处相切,
而过A(2,2)且与切线l垂直的直线方程为y-2=- (x-2),
(x-2),
令y=0,得x=6,得圆心(6,0),
∴圆的半径是r=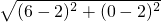 =
=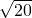 ,
,
则圆C的方程为 (x-6)2+y2=20.
故答案为:(x-6)2+y2=20.
点评:本题主要考查直线与圆的位置关系.考查导数的几何意义,即函数在某点的导数值等于过该点的曲线的切线的斜率.

分析:先对函数进行求导,根据导函数在点A处的值为切线的斜率可得切线方程,再利用直线与圆相切求出圆心坐标及、半径即可得出答案.
解答:∵y=
 x2∴y'=x
x2∴y'=x当x=2时,y'=2,
∴点A(2,2)处的切线方程为:y-2=2(x-2)即:2x-y-2=0
∵切线l恰与圆C在A点处相切,
而过A(2,2)且与切线l垂直的直线方程为y-2=-
 (x-2),
(x-2),令y=0,得x=6,得圆心(6,0),
∴圆的半径是r=
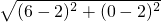 =
=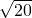 ,
,则圆C的方程为 (x-6)2+y2=20.
故答案为:(x-6)2+y2=20.
点评:本题主要考查直线与圆的位置关系.考查导数的几何意义,即函数在某点的导数值等于过该点的曲线的切线的斜率.



