已知f•|x-1|.若关于x的方程f(x)=x+m有三个不同的实数解.则实数m的取值范围 .
已知f(x)=(x+1)•|x-1|,若关于x的方程f(x)=x+m有三个不同的实数解,则实数m的取值范围________.在线课程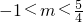
分析:通过对x-1≥0与x<0的讨论,去掉f(x)=(x+1)•|x-1|的绝对值符号,并作出其图象,数形结合即可解决.
解答: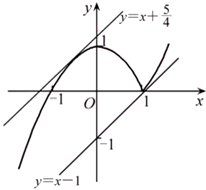 解:由f(x)=(x+1)|x-1|=
解:由f(x)=(x+1)|x-1|=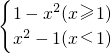
得函数y=f(x)的图象(如图).
由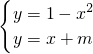 得x2+x+m-1=0,
得x2+x+m-1=0,
∴△=1-4(m-1)=5-4m,
由△=0,得m=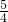 ,
,
∴由其图象可知f(x)=x+m有三个不同的实数解,就是直线y=x+m与抛物线
f(x)=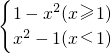 有三个交点,由图可知-1<m<
有三个交点,由图可知-1<m<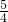 ,
,
∴实数m的取值范围是-1<m<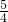 .
.
故答案为:-1<m<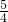 .
.
点评:本题考查带绝对值的函数,难点在于作f(x)=(x+1)•|x-1|与y=x+m的图象,突出转化思想与数形结合思想的考查,属于中档题.

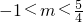
分析:通过对x-1≥0与x<0的讨论,去掉f(x)=(x+1)•|x-1|的绝对值符号,并作出其图象,数形结合即可解决.
解答:
 解:由f(x)=(x+1)|x-1|=
解:由f(x)=(x+1)|x-1|=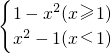
得函数y=f(x)的图象(如图).
由
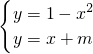 得x2+x+m-1=0,
得x2+x+m-1=0,∴△=1-4(m-1)=5-4m,
由△=0,得m=
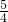 ,
,∴由其图象可知f(x)=x+m有三个不同的实数解,就是直线y=x+m与抛物线
f(x)=
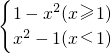 有三个交点,由图可知-1<m<
有三个交点,由图可知-1<m<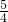 ,
,∴实数m的取值范围是-1<m<
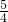 .
.故答案为:-1<m<
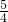 .
.点评:本题考查带绝对值的函数,难点在于作f(x)=(x+1)•|x-1|与y=x+m的图象,突出转化思想与数形结合思想的考查,属于中档题.



