已知函数f(x)=x2.集合A={x|f(x-1)=ax.x∈R}.且A∪{x|x是正实数}={x|x是正实数}.则实数a的取值范围是 ．
已知函数f（x）=x2，集合A={x|f（x-1）=ax，x∈R}，且A∪{x|x是正实数}={x|x是正实数}，则实数a的取值范围是________．在线课程（-4，+∞）
分析：先对集合A进行化简，要使A∪{x|x是正实数}={x|x是正实数}，只需x2-（2+a）x+1=0只有正实数解，然后将参数a分离出来，最后利用均值不等式求出a的范围即可．
解答：∵f（x）=x2，f（x-1）=ax
∴f（x-1）=（x-1）2=ax，即x2-（2+a）x+1=0
∵A∪{x|x是正实数}={x|x是正实数}，
∴x2-（2+a）x+1=0只有正实数解或此方程无解
若A中只有正实数解，即2+a=x+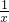
≥2，∴a≥0即[0，+∞）
若A是空集，则方程x2-（2+a）x+1=0无解，可得（2+a）2-4＜0，得-4＜a＜0
故答案为（-4，+∞）．
点评：本题以一元二次方程为载体主要考查了集合的并集运算，以及均值不等式的运用，考查函数与方程的思想，属于基础题．
分析：先对集合A进行化简，要使A∪{x|x是正实数}={x|x是正实数}，只需x2-（2+a）x+1=0只有正实数解，然后将参数a分离出来，最后利用均值不等式求出a的范围即可．
解答：∵f（x）=x2，f（x-1）=ax
∴f（x-1）=（x-1）2=ax，即x2-（2+a）x+1=0
∵A∪{x|x是正实数}={x|x是正实数}，
∴x2-（2+a）x+1=0只有正实数解或此方程无解
若A中只有正实数解，即2+a=x+
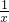≥2，∴a≥0即[0，+∞）若A是空集，则方程x2-（2+a）x+1=0无解，可得（2+a）2-4＜0，得-4＜a＜0
故答案为（-4，+∞）．
点评：本题以一元二次方程为载体主要考查了集合的并集运算，以及均值不等式的运用，考查函数与方程的思想，属于基础题．
