已知点P.A.B.C是球O表面上的四个点.且PA.PB.PC两两成60°角.PA=PB=PC=1cm.则球的表面积为 cm2.
已知点P,A,B,C是球O表面上的四个点,且PA,PB,PC两两成60°角,PA=PB=PC=1cm,则球的表面积为________cm2.在线课程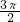
分析:判断四面体是正四面体,正四面体扩展为正方体,它们的外接球是同一个球,正方体的对角线长就是球的直径,求出直径即可求出球的表面积.
解答:因为点P,A,B,C是球O表面上的四个点,且PA,PB,PC两两成60°角,PA=PB=PC=1cm,
所以四面体是正四面体,正四面体扩展为正方体,它们的外接球是同一个球,正方体的棱长为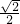 ,
,
正方体的对角线长就是球的直径,正方体的对角线长为: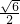 ,
,
所以球的表面积为:4πR2=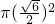 =
=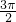 (cm2)
(cm2)
故答案为: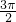 .
.
点评:本题是中档题,考查正四面体的外接球,球的表面积的求法,本题的突破口在正四面体转化为正方体,外接球是同一个球,考查计算能力转化思想以及空间想象能力.

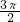
分析:判断四面体是正四面体,正四面体扩展为正方体,它们的外接球是同一个球,正方体的对角线长就是球的直径,求出直径即可求出球的表面积.
解答:因为点P,A,B,C是球O表面上的四个点,且PA,PB,PC两两成60°角,PA=PB=PC=1cm,
所以四面体是正四面体,正四面体扩展为正方体,它们的外接球是同一个球,正方体的棱长为
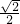 ,
,正方体的对角线长就是球的直径,正方体的对角线长为:
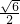 ,
,所以球的表面积为:4πR2=
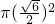 =
=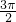 (cm2)
(cm2)故答案为:
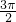 .
.点评:本题是中档题,考查正四面体的外接球,球的表面积的求法,本题的突破口在正四面体转化为正方体,外接球是同一个球,考查计算能力转化思想以及空间想象能力.



