一次研究性课堂上.老师给出函数.甲.乙.丙三位同学在研究此函数时分别给出命题:甲:函数f,乙:若x1≠x2则一定有f(x1)≠f(x2),丙:若规定f1.fn(x)=f(f1(x)).则fn(x)=.
一次研究性课堂上，老师给出函数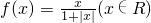
，甲、乙、丙三位同学在研究此函数时分别给出命题：
甲：函数f（x）的值域为（-1，1）；
乙：若x1≠x2则一定有f（x1）≠f（x2）；
丙：若规定f1（x）=f（x），fn（x）=f（f1（x）），则fn（x）=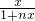
，对任意的n∈N*恒成立
你认为上述三个命题中正确的个数有
A.3个B.2个C.1个D.0个在线课程B
分析：利用奇函数的定义判断出f（x）为奇函数，通过对x的分段讨论去掉绝对值转化为分段函数，讨论x≥0的值域、单调性判断出甲、乙说的对利用已知的递推关系求出fn（x），判断出丙的说法不对．
解答：∵f（-x）-f（x）
∴f（x）为奇函数
∵
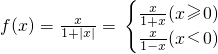
当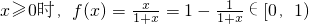
∵f（x）为奇函数，
∴当x＜0是，f（x）∈（-1，0）
总之，f（x）∈（-1，1）
故甲对
当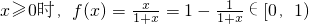为增函数，
∵f（x）为奇函数
∴当x＜0是，f（x）∈（-1，0）为增函数
所以f（x在（-1，1）上为增函数
故乙对
fn（x）=f（f1（x））=f（f（x）=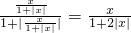
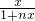=不恒成立
故丙不对
故选B
点评：通过对自变量分段讨论将含绝对值的函数转化为分段函数，解决分段函数的性质问题一般分段讨论研究．
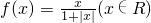，甲、乙、丙三位同学在研究此函数时分别给出命题：甲：函数f（x）的值域为（-1，1）；
乙：若x1≠x2则一定有f（x1）≠f（x2）；
丙：若规定f1（x）=f（x），fn（x）=f（f1（x）），则fn（x）=
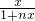，对任意的n∈N*恒成立你认为上述三个命题中正确的个数有
A.3个B.2个C.1个D.0个在线课程B
分析：利用奇函数的定义判断出f（x）为奇函数，通过对x的分段讨论去掉绝对值转化为分段函数，讨论x≥0的值域、单调性判断出甲、乙说的对利用已知的递推关系求出fn（x），判断出丙的说法不对．
解答：∵f（-x）-f（x）
∴f（x）为奇函数
∵
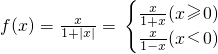
当
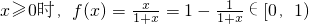
∵f（x）为奇函数，
∴当x＜0是，f（x）∈（-1，0）
总之，f（x）∈（-1，1）
故甲对
当
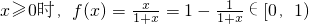为增函数，∵f（x）为奇函数
∴当x＜0是，f（x）∈（-1，0）为增函数
所以f（x在（-1，1）上为增函数
故乙对
fn（x）=f（f1（x））=f（f（x）=
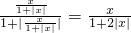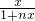=不恒成立故丙不对
故选B
点评：通过对自变量分段讨论将含绝对值的函数转化为分段函数，解决分段函数的性质问题一般分段讨论研究．
