某种产品每件成本为6元.每件售价为x元.年销量为u万件.若已知与成正比.且售价为10元时.年销量为28万件.(1)求年销售利润y关于x的函数关系式.(2)求售价为多少时.年利润最大.并求出最大年利润.
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知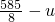 与
与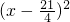 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式.(2)求售价为多少时,年利润最大,并求出最大年利润.在线课程解:(1)设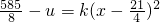 ,
,
∵售价为10元时,年销量为28万件;
∴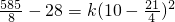 ,解得k=2.
,解得k=2.
∴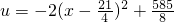 =-2x2+21x+18.
=-2x2+21x+18.
∴y=(-2x2+21x+18)(x-6)=-2x3+33x2-108x-108.
(2)y'=-6x2+66x-108=-6(x2-11x+18)=-6(x-2)(x-9)
令y'=0得x=2(∵x>6,舍去)或x=9
显然,当x∈(6,9)时,y'>0当x∈(9,+∞)时,y'<0
∴函数y=-2x3+33x2-108x-108在(6,9)上是关于x的增函数;
在(9,+∞)上是关于x的减函数.
∴当x=9时,y取最大值,且ymax=135.
∴售价为9元时,年利润最大,最大年利润为135万元.
分析:(1)根据题中条件:“若已知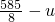 与
与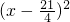 成正比”可设
成正比”可设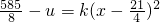 ,再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.
,再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.
(2)利用导数研究函数的最值,先求出y的导数,根据y′>0求得的区间是单调增区间,y′<0求得的区间是单调减区间,从而求出极值进而得出最值即可.
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.属于基础题.

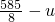 与
与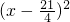 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.(1)求年销售利润y关于x的函数关系式.(2)求售价为多少时,年利润最大,并求出最大年利润.在线课程解:(1)设
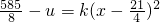 ,
,∵售价为10元时,年销量为28万件;
∴
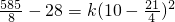 ,解得k=2.
,解得k=2.∴
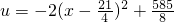 =-2x2+21x+18.
=-2x2+21x+18.∴y=(-2x2+21x+18)(x-6)=-2x3+33x2-108x-108.
(2)y'=-6x2+66x-108=-6(x2-11x+18)=-6(x-2)(x-9)
令y'=0得x=2(∵x>6,舍去)或x=9
显然,当x∈(6,9)时,y'>0当x∈(9,+∞)时,y'<0
∴函数y=-2x3+33x2-108x-108在(6,9)上是关于x的增函数;
在(9,+∞)上是关于x的减函数.
∴当x=9时,y取最大值,且ymax=135.
∴售价为9元时,年利润最大,最大年利润为135万元.
分析:(1)根据题中条件:“若已知
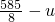 与
与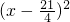 成正比”可设
成正比”可设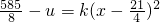 ,再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.
,再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.(2)利用导数研究函数的最值,先求出y的导数,根据y′>0求得的区间是单调增区间,y′<0求得的区间是单调减区间,从而求出极值进而得出最值即可.
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.属于基础题.



