已知.-g(x)存在单调递减区间.求实数a的取值范围,(Ⅱ)当a=-1时.求证:x≤eg(x)-2在成立-x的最大值.并证明当n>2.n∈N*时.
已知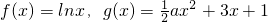 ,
,
(Ⅰ)若函数h(x)=f(x)-g(x)存在单调递减区间,求实数a的取值范围;
(Ⅱ)当a=-1时,求证:x≤eg(x)-2在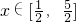 成立
成立
(Ⅲ)求f(x)-x的最大值,并证明当n>2,n∈N*时,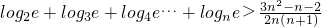 (e为自然对数lnx的底数)在线课程(Ⅰ)解:函数
(e为自然对数lnx的底数)在线课程(Ⅰ)解:函数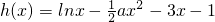
所以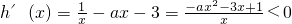 在(0,+∞)上有解,
在(0,+∞)上有解,
即ax2+3x-1>0在(0,+∞)上有解,由ax2+3x-1>0得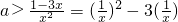
因为当x>0,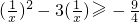
所以a的范围是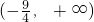 …(4分)
…(4分)
(Ⅱ)证明:原不等式即为f(x)<g(x)-2,构造函数φ(x)=f(x)-g(x)+2
∴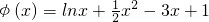 ∴
∴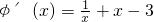 ,
,
∴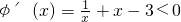 对于
对于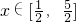 恒成立,
恒成立,
∴φ(x)单调递增
∴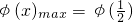 =
=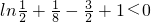
∴f(x)<g(x)-2
∴x≤eg(x)-2在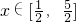 成立,原不等式得证 …(9分)
成立,原不等式得证 …(9分)
(Ⅲ)解:∵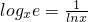 ,令m(x)=f(x)-x=lnx-x,
,令m(x)=f(x)-x=lnx-x,
∴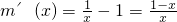
所以函数m(x)在(0,1)上递增,在(1,+∞)上递减,
所以m(x)≤m(1),即f(x)-x的最大值为-1
证明:由m(x)≤m(1)得lnx≤-1+x
∴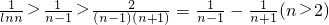 ,
,
∴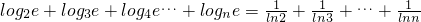
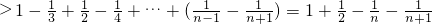 =
=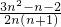 …(14分)
…(14分)
分析:(Ⅰ)函数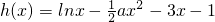 ,函数h(x)=f(x)-g(x)存在单调递减区间,等价于
,函数h(x)=f(x)-g(x)存在单调递减区间,等价于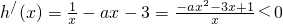 在(0,+∞)上有解,即ax2+3x-1>0在(0,+∞)上有解,再利用分离参数法,即可求得a的范围;
在(0,+∞)上有解,即ax2+3x-1>0在(0,+∞)上有解,再利用分离参数法,即可求得a的范围;
(Ⅱ)原不等式即为f(x)<g(x)-2,构造函数φ(x)=f(x)-g(x)+2,可确定φ(x)单调递增,从而原不等式得证;
(Ⅲ)根据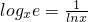 ,令m(x)=f(x)-x=lnx-x,利用导数可知函数m(x)在(0,1)上递增,在(1,+∞)上递减,从而可得f(x)-x的最大值为-1,进而可得lnx≤-1+x,再利用放缩法即可证得.
,令m(x)=f(x)-x=lnx-x,利用导数可知函数m(x)在(0,1)上递增,在(1,+∞)上递减,从而可得f(x)-x的最大值为-1,进而可得lnx≤-1+x,再利用放缩法即可证得.
点评:本题重点考查导数知识的运用,考查利用导数研究函数的单调性,证明不等式,考查放缩法的运用,综合性比较强.

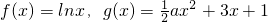 ,
,(Ⅰ)若函数h(x)=f(x)-g(x)存在单调递减区间,求实数a的取值范围;
(Ⅱ)当a=-1时,求证:x≤eg(x)-2在
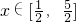 成立
成立(Ⅲ)求f(x)-x的最大值,并证明当n>2,n∈N*时,
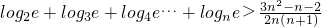 (e为自然对数lnx的底数)在线课程(Ⅰ)解:函数
(e为自然对数lnx的底数)在线课程(Ⅰ)解:函数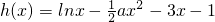
所以
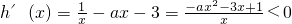 在(0,+∞)上有解,
在(0,+∞)上有解,即ax2+3x-1>0在(0,+∞)上有解,由ax2+3x-1>0得
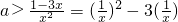
因为当x>0,
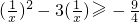
所以a的范围是
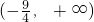 …(4分)
…(4分)(Ⅱ)证明:原不等式即为f(x)<g(x)-2,构造函数φ(x)=f(x)-g(x)+2
∴
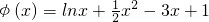 ∴
∴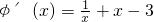 ,
,∴
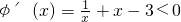 对于
对于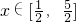 恒成立,
恒成立,∴φ(x)单调递增
∴
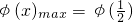 =
=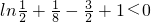
∴f(x)<g(x)-2
∴x≤eg(x)-2在
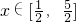 成立,原不等式得证 …(9分)
成立,原不等式得证 …(9分)(Ⅲ)解:∵
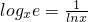 ,令m(x)=f(x)-x=lnx-x,
,令m(x)=f(x)-x=lnx-x,∴
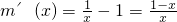
所以函数m(x)在(0,1)上递增,在(1,+∞)上递减,
所以m(x)≤m(1),即f(x)-x的最大值为-1
证明:由m(x)≤m(1)得lnx≤-1+x
∴
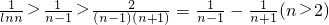 ,
,∴
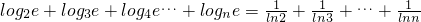
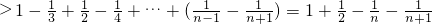 =
=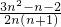 …(14分)
…(14分)分析:(Ⅰ)函数
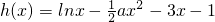 ,函数h(x)=f(x)-g(x)存在单调递减区间,等价于
,函数h(x)=f(x)-g(x)存在单调递减区间,等价于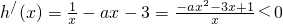 在(0,+∞)上有解,即ax2+3x-1>0在(0,+∞)上有解,再利用分离参数法,即可求得a的范围;
在(0,+∞)上有解,即ax2+3x-1>0在(0,+∞)上有解,再利用分离参数法,即可求得a的范围;(Ⅱ)原不等式即为f(x)<g(x)-2,构造函数φ(x)=f(x)-g(x)+2,可确定φ(x)单调递增,从而原不等式得证;
(Ⅲ)根据
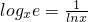 ,令m(x)=f(x)-x=lnx-x,利用导数可知函数m(x)在(0,1)上递增,在(1,+∞)上递减,从而可得f(x)-x的最大值为-1,进而可得lnx≤-1+x,再利用放缩法即可证得.
,令m(x)=f(x)-x=lnx-x,利用导数可知函数m(x)在(0,1)上递增,在(1,+∞)上递减,从而可得f(x)-x的最大值为-1,进而可得lnx≤-1+x,再利用放缩法即可证得.点评:本题重点考查导数知识的运用,考查利用导数研究函数的单调性,证明不等式,考查放缩法的运用,综合性比较强.



