设f(x)=sin4x-sinxcosx+cos4x.则f(x)的值域是 .
设f(x)=sin4x-sinxcosx+cos4x,则f(x)的值域是________.在线课程[0,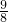 ]
]
分析:t=sin2x,-1≤t≤1,化简f(x)的解析式为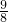 -
- (t+
(t+ )2 ,再利用二次函数的性质求出f(x)的值域.
)2 ,再利用二次函数的性质求出f(x)的值域.
解答:f(x)=sin4x-sinxcosx+cos4x=1- sin2x-
sin2x- sin22x. 令t=sin2x,
sin22x. 令t=sin2x,
则f(x)=g(t)=1- t-
t- t2 =
t2 =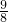 -
- (t+
(t+ )2 ,且-1≤t≤1.
)2 ,且-1≤t≤1.
故当t=- 时,f(x)取得最大值为
时,f(x)取得最大值为 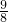 ,当t=1时,f(x)取得最小值为 0,
,当t=1时,f(x)取得最小值为 0,
故,f(x)∈[0,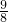 ],即 f(x)的值域是[0,
],即 f(x)的值域是[0,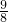 ],
],
故答案为[0,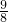 ].
].
点评:本题主要考查三角函数的恒等变换及化简求值,二次函数的性质的应用,属于中档题.

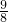 ]
]分析:t=sin2x,-1≤t≤1,化简f(x)的解析式为
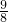 -
- (t+
(t+ )2 ,再利用二次函数的性质求出f(x)的值域.
)2 ,再利用二次函数的性质求出f(x)的值域.解答:f(x)=sin4x-sinxcosx+cos4x=1-
 sin2x-
sin2x- sin22x. 令t=sin2x,
sin22x. 令t=sin2x,则f(x)=g(t)=1-
 t-
t- t2 =
t2 =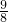 -
- (t+
(t+ )2 ,且-1≤t≤1.
)2 ,且-1≤t≤1.故当t=-
 时,f(x)取得最大值为
时,f(x)取得最大值为 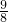 ,当t=1时,f(x)取得最小值为 0,
,当t=1时,f(x)取得最小值为 0,故,f(x)∈[0,
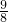 ],即 f(x)的值域是[0,
],即 f(x)的值域是[0,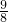 ],
],故答案为[0,
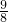 ].
].点评:本题主要考查三角函数的恒等变换及化简求值,二次函数的性质的应用,属于中档题.



