如图.在直三棱柱ABC-A1B1C1中.∠ACB=90°.AC=BC=CC1=2．(1)证明:AB1⊥BC1,(2)求点B到平面AB1C1的距离,(3)求二面角C1-AB1-A1的大小．

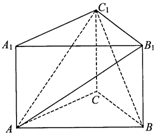如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=BC=CC₁=2．
（1）证明：AB₁⊥BC₁；
（2）求点B到平面AB₁C₁的距离；
（3）求二面角C₁-AB₁-A₁的大小．在线课程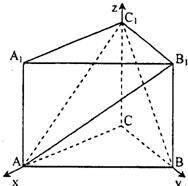证明：（1）如图建立直角坐标系，其为C为坐标原点，
题意A（2，0，0），B（0，2，0），A₁（2，0，2），B₁（0，2，2），C₁（0，0，2）．
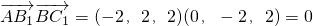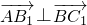∵，∴∴AB₁⊥BC₁
解：（2）设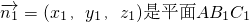的一个法向量，
由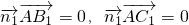得
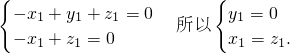
令
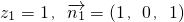
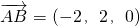∵，∴点B到平面AB₁C₁的距离．
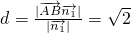（3）解设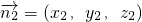是平面A₁AB₁的一个法向量
由
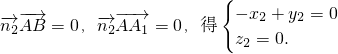
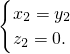∴令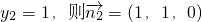
∵，
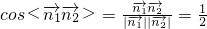∴二面角C₁-AB-A₁的大小为60°．
分析：（1）以C点为坐标原点，CA，CB，CC₁为X，Y，Z轴正方向建立空间坐标系，分别求出AB₁与BC₁的方向向量，代入数量积公式，得到其数量积为0，即可得到AB₁⊥BC₁；
（2）求出平面AB₁C₁的一个法向量，则AB的方向向量，代入到公式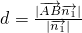，即可求出
点B到平面AB₁C₁的距离；
（3）结合（2）的结合，再求出平面AB₁A₁的一个法向量，代入向量夹角公式，即可得到二面角C₁-AB₁-A₁的大小．
点评：本题考查的知识点是二面角的平面角及求法，点到面的距离，异面直线的夹角，其中建立适当的空间坐标系，将问题转化为向量夹角及向量长度问题是解答本题的关键．