已知函数f(x)是定义在R上的奇函数.f(2)=0.当x>0时.有xf′<0成立.则不等式x2•f(x)>0的解集是A.B.C.D.
已知函数f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有xf′(x)-f(x)<0成立,则不等式x2•f(x)>0的解集是
A.(-2,0)∪(2,+∞)B.(-∞,-2)∪(2,+∞)C.(-2,0)∪(0,2)D.(-∞,-2)∪(0,2)在线课程D
分析:令g(x)=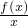 ,依题意,可求得0<x<2或x<-2时f(x)>0,从而可求得不等式x2•f(x)>0的解集.
,依题意,可求得0<x<2或x<-2时f(x)>0,从而可求得不等式x2•f(x)>0的解集.
解答: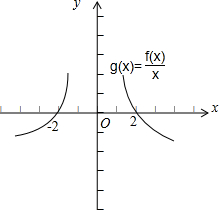 解:g(x)=
解:g(x)=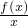 ,
,
则g′(x)=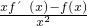 ,
,
∵当x>0时,有xf′(x)-f(x)<0成立,
∴当x>0时,g′(x)<0,
∴g(x)=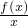 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
∵函数f(x)是定义在R上的奇函数,f(2)=0,
∴g(-x)=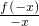 =
=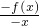 =g(x),
=g(x),
∴g(x)为偶函数,且g(2)=0,
∴当0<x<2时,g(x)>0,于是此时f(x)>0;
同理可得,当x<-2时,g(x)<0,于是此时f(x)>0;
∴f(x)>0的解集为{x|x<-2或0<x<2}
∴不等式x2•f(x)>0的解集就是f(x)>0的解集,为{x|x<-2或0<x<2}.
故选D.
点评:本题考查利用导数研究函数的单调性,考查函数的奇偶性与单调性,考查分析与作图能力,属于中档题.

A.(-2,0)∪(2,+∞)B.(-∞,-2)∪(2,+∞)C.(-2,0)∪(0,2)D.(-∞,-2)∪(0,2)在线课程D
分析:令g(x)=
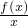 ,依题意,可求得0<x<2或x<-2时f(x)>0,从而可求得不等式x2•f(x)>0的解集.
,依题意,可求得0<x<2或x<-2时f(x)>0,从而可求得不等式x2•f(x)>0的解集.解答:
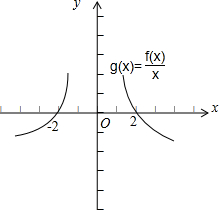 解:g(x)=
解:g(x)=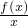 ,
,则g′(x)=
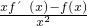 ,
,∵当x>0时,有xf′(x)-f(x)<0成立,
∴当x>0时,g′(x)<0,
∴g(x)=
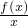 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,∵函数f(x)是定义在R上的奇函数,f(2)=0,
∴g(-x)=
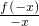 =
=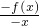 =g(x),
=g(x),∴g(x)为偶函数,且g(2)=0,
∴当0<x<2时,g(x)>0,于是此时f(x)>0;
同理可得,当x<-2时,g(x)<0,于是此时f(x)>0;
∴f(x)>0的解集为{x|x<-2或0<x<2}
∴不等式x2•f(x)>0的解集就是f(x)>0的解集,为{x|x<-2或0<x<2}.
故选D.
点评:本题考查利用导数研究函数的单调性,考查函数的奇偶性与单调性,考查分析与作图能力,属于中档题.



