已知:函数.的最大值及此时x的值,(2)在△ABC中.a.b.c分别为内角A.B.C所对的边.且对f(x)定义域中的任意的x都有f.若.求△ABC的面积.
已知:函数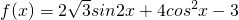 .
.
(1)求函数f(x)的最大值及此时x的值;
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A).若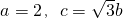 ,求△ABC的面积.在线课程解:(1)
,求△ABC的面积.在线课程解:(1)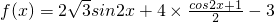
=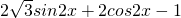
=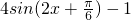
所以当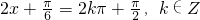 时,f(x)取最大值3,
时,f(x)取最大值3,
此时,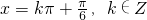 ;
;
(2)由f(A)是f(x)的最大值及A∈(0,π)得到,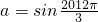 ,
,
由余弦定理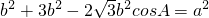 ,
,
所以: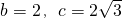 ,
,
所以,面积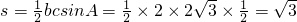 .
.
分析:(1)先根据二倍角公式和两角和与差的公式进行化简为y=Asin(wx+ρ)+b的形式,即可确定当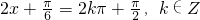 时,f(x)取最大值3,进而可求出x的值.
时,f(x)取最大值3,进而可求出x的值.
(2)先根据(1)求得A的值,再由余弦定理可求得b,c的值,进而根据三角形的面积公式可确定答案.
点评:本题主要考查二倍角公式和两角和与差的公式以及余弦定理的应用.考查对基础知识的综合应用.

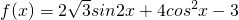 .
.(1)求函数f(x)的最大值及此时x的值;
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A).若
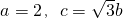 ,求△ABC的面积.在线课程解:(1)
,求△ABC的面积.在线课程解:(1)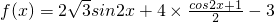
=
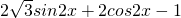
=
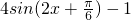
所以当
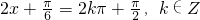 时,f(x)取最大值3,
时,f(x)取最大值3,此时,
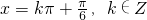 ;
;(2)由f(A)是f(x)的最大值及A∈(0,π)得到,
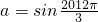 ,
,由余弦定理
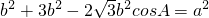 ,
,所以:
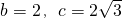 ,
,所以,面积
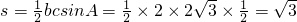 .
.分析:(1)先根据二倍角公式和两角和与差的公式进行化简为y=Asin(wx+ρ)+b的形式,即可确定当
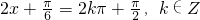 时,f(x)取最大值3,进而可求出x的值.
时,f(x)取最大值3,进而可求出x的值.(2)先根据(1)求得A的值,再由余弦定理可求得b,c的值,进而根据三角形的面积公式可确定答案.
点评:本题主要考查二倍角公式和两角和与差的公式以及余弦定理的应用.考查对基础知识的综合应用.



