互不相等的三个数之积是-8.这三个数适当排列后可成为等比数列.又可成为等差数列.求这三个数排成的等差数列．
互不相等的三个数之积是-8，这三个数适当排列后可成为等比数列，又可成为等差数列，求这三个数排成的等差数列．在线课程解：由题意设这三个数为：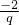
，-2，-2q，
（1）若-2为等差中项，则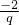+（-2q）=-4，即1+q2=2q，解得q=1，与三个数互不相等矛盾；
（2）若-2q为等差中项，则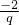+（-2）=-4q，即2q2-q-1=0，解得q=1，或q=
，
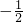由（1）知q=1应舍去，当q=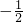时，三个数为：-2，1，4，符合题意；
（3）若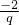是等差中项，则
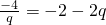，即q2+q-2=0，解得q=-2，或q=1（舍去），
故当q=-2时，这三个数为4，1，-2，
综上所述，这三个数排成的等差数列是4，1，-2或者-2，1，4
分析：由题意设这三个数为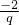：，-2，-2q，分别让它们为等差中项讨论可得答案．
点评：本题考查等差数列与等比数列的综合应用，涉及分类讨论的思想，属基础题．
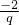，-2，-2q，（1）若-2为等差中项，则
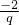+（-2q）=-4，即1+q2=2q，解得q=1，与三个数互不相等矛盾；（2）若-2q为等差中项，则
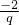+（-2）=-4q，即2q2-q-1=0，解得q=1，或q=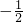，由（1）知q=1应舍去，当q=
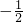时，三个数为：-2，1，4，符合题意；（3）若
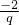是等差中项，则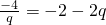，即q2+q-2=0，解得q=-2，或q=1（舍去），故当q=-2时，这三个数为4，1，-2，
综上所述，这三个数排成的等差数列是4，1，-2或者-2，1，4
分析：由题意设这三个数为：
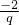，-2，-2q，分别让它们为等差中项讨论可得答案．点评：本题考查等差数列与等比数列的综合应用，涉及分类讨论的思想，属基础题．
