数列 1.2.3.4.5.-.的前n项之和等于 .
数列 1 ,2
,2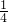 ,3
,3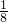 ,4
,4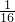 ,5
,5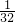 ,…,的前n项之和等于________.在线课程
,…,的前n项之和等于________.在线课程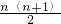 +1-
+1-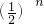
分析:由题意得到数列的通项公式为:an=n+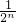 ,然后把和表示为=(1+2+3+…+n)+(
,然后把和表示为=(1+2+3+…+n)+(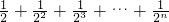 ),分别求和即可.
),分别求和即可.
解答:由题意可知数列的通项公式为:an=n+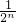
故前n项之和为:(1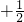 )+(2
)+(2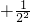 )+(3
)+(3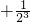 )+…+(n
)+…+(n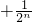 )
)
=(1+2+3+…+n)+(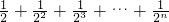 )
)
=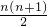 +
+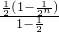
=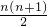 +1-
+1-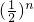
故答案为: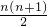 +1-
+1-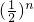
点评:本题为数列的求和问题,得出数列的通项并正确用公式是解决问题的关键,属中档题.

 ,2
,2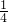 ,3
,3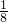 ,4
,4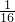 ,5
,5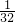 ,…,的前n项之和等于________.在线课程
,…,的前n项之和等于________.在线课程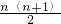 +1-
+1-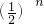
分析:由题意得到数列的通项公式为:an=n+
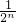 ,然后把和表示为=(1+2+3+…+n)+(
,然后把和表示为=(1+2+3+…+n)+(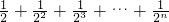 ),分别求和即可.
),分别求和即可.解答:由题意可知数列的通项公式为:an=n+
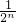
故前n项之和为:(1
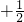 )+(2
)+(2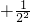 )+(3
)+(3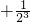 )+…+(n
)+…+(n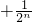 )
)=(1+2+3+…+n)+(
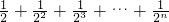 )
)=
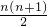 +
+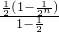
=
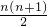 +1-
+1-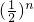
故答案为:
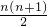 +1-
+1-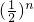
点评:本题为数列的求和问题,得出数列的通项并正确用公式是解决问题的关键,属中档题.



