我们把使得f(x)=0的实数x叫做函数y=f(x)的零点.对于区间[a.b]上的连续函数y=f<0.那么函数y=f内有零点.则函数f(x)=lnx+2x-6的零点个数为A.0B.1C.2D.多于两个
我们把使得f(x)=0的实数x叫做函数y=f(x)的零点.对于区间[a,b]上的连续函数y=f(x),若f(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.则函数f(x)=lnx+2x-6的零点个数为
A.0B.1C.2D.多于两个在线课程B
分析:求导函数,确定函数的单调性,再用零点存在定理,就可以得出结论.
解答:函数的定义域为(0,+∞)
求导函数可得: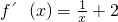 ,∴f′(x)>0
,∴f′(x)>0
∴函数为单调增函数
∵f(2)=ln2-2<0,f(3)=ln3>0
∴函数在(2,3)上存在唯一零点
故选B.
点评:函数零点的判断,只要满足区间[a,b]上的连续函数y=f(x),若f(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.

A.0B.1C.2D.多于两个在线课程B
分析:求导函数,确定函数的单调性,再用零点存在定理,就可以得出结论.
解答:函数的定义域为(0,+∞)
求导函数可得:
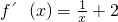 ,∴f′(x)>0
,∴f′(x)>0∴函数为单调增函数
∵f(2)=ln2-2<0,f(3)=ln3>0
∴函数在(2,3)上存在唯一零点
故选B.
点评:函数零点的判断,只要满足区间[a,b]上的连续函数y=f(x),若f(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.



