“m=-1 是“直线l1:x+my+6=0与l2:(m-2)x+3y+2m=0互相平行 的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
“m=-1”是“直线l1：x+my+6=0与l2：（m-2）x+3y+2m=0互相平行”的
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件在线课程C
分析：当m=-1时，经检验，两直线平行，当两直线平行时，由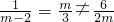
可得m=-1．利用充要条件的定义可得结论．
解答：当m=-1时，直线l1：x+my+6=0 即 x-y+6=0．l2：（m-2）x+3y+2m=0 即-3x+3y-2=0，即 x-y+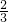
=0，
显然，两直线平行．
当直线l1：x+my+6=0与l2：（m-2）x+3y+2m=0互相平行时，由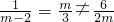 可得m=-1．
故“m=-1”是“直线l1：x+my+6=0与l2：（m-2）x+3y+2m=0互相平行”的充要条件，
故选 C．
点评：本题考查两直线平行的性质，充要条件的定义，两直线平行，一次项系数之比相等，但不等于常数项之比．
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件在线课程C
分析：当m=-1时，经检验，两直线平行，当两直线平行时，由
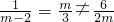可得m=-1．利用充要条件的定义可得结论．解答：当m=-1时，直线l1：x+my+6=0 即 x-y+6=0．l2：（m-2）x+3y+2m=0 即-3x+3y-2=0，即 x-y+
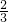=0，显然，两直线平行．
当直线l1：x+my+6=0与l2：（m-2）x+3y+2m=0互相平行时，由
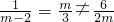可得m=-1．故“m=-1”是“直线l1：x+my+6=0与l2：（m-2）x+3y+2m=0互相平行”的充要条件，
故选 C．
点评：本题考查两直线平行的性质，充要条件的定义，两直线平行，一次项系数之比相等，但不等于常数项之比．
