某地区预计从2011年初开始的第x月.商品A的价格(x∈N.x≤12.价格单位:元).且第x月该商品的销售量g.(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?
某地区预计从2011年初开始的第x月,商品A的价格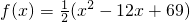 (x∈N,x≤12,价格单位:元),且第x月该商品的销售量g(x)=x+12(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?在线课程解:(1)∵价格函数为:
(x∈N,x≤12,价格单位:元),且第x月该商品的销售量g(x)=x+12(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?在线课程解:(1)∵价格函数为: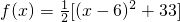 ,(x∈N,1≤x≤12),∴当x=6时,f(x)取得最小值,
,(x∈N,1≤x≤12),∴当x=6时,f(x)取得最小值,
即第6月的价格最低,最低价格为16.5元;
(2)设第x月的销售收入为y(万元),依题意有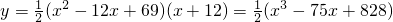 ,
,
对y求导,得: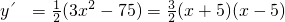 ,
,
所以,当1≤x≤5时,y'≤0,y递减;
当5≤x≤12时,y'≥0,y递增,
所以,当x=5时,y最小,即第5个月销售收入最少;
答:2011年在第5月的销售收入最低.
分析:(1)由价格函数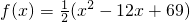 (x∈N,1≤x≤12)是二次函数,可得f(x)的最小值,即价格最低;
(x∈N,1≤x≤12)是二次函数,可得f(x)的最小值,即价格最低;
(2)销售收入y=f(x)•g(x),整理,得关于x的三次函数,用求导法,可以求出y的最小值,即哪个月销售收入最少;
点评:本题考查了二次函数,三次函数模型的应用,利用求导法求函数的最值时,常用“导数大于0,函数单调增;导数小于0,函数单调减”来判定.

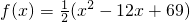 (x∈N,x≤12,价格单位:元),且第x月该商品的销售量g(x)=x+12(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?在线课程解:(1)∵价格函数为:
(x∈N,x≤12,价格单位:元),且第x月该商品的销售量g(x)=x+12(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?在线课程解:(1)∵价格函数为: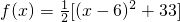 ,(x∈N,1≤x≤12),∴当x=6时,f(x)取得最小值,
,(x∈N,1≤x≤12),∴当x=6时,f(x)取得最小值,即第6月的价格最低,最低价格为16.5元;
(2)设第x月的销售收入为y(万元),依题意有
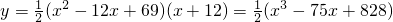 ,
,对y求导,得:
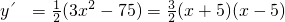 ,
,所以,当1≤x≤5时,y'≤0,y递减;
当5≤x≤12时,y'≥0,y递增,
所以,当x=5时,y最小,即第5个月销售收入最少;
答:2011年在第5月的销售收入最低.
分析:(1)由价格函数
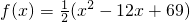 (x∈N,1≤x≤12)是二次函数,可得f(x)的最小值,即价格最低;
(x∈N,1≤x≤12)是二次函数,可得f(x)的最小值,即价格最低;(2)销售收入y=f(x)•g(x),整理,得关于x的三次函数,用求导法,可以求出y的最小值,即哪个月销售收入最少;
点评:本题考查了二次函数,三次函数模型的应用,利用求导法求函数的最值时,常用“导数大于0,函数单调增;导数小于0,函数单调减”来判定.



