已知正四面体ABCD内一点P.满足PA=PB=.PC=PD=3.则该四面体的棱长是A.4B.2C.4D.8
已知正四面体ABCD内一点P，满足PA=PB=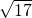
，PC=PD=3，则该四面体的棱长是
A.4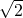
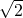B.2C.4D.8在线课程A
分析：取AB，CD的中点E，F，则EF⊥AB，EF⊥CD，且P在EF上，设出棱长，建立方程，即可求得结论．
解答：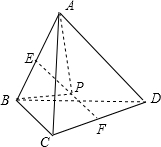
解：取AB，CD的中点E，F，则EF⊥AB，EF⊥CD，且P在EF上
设四面体的棱长是2a，则EF=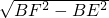
=
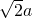
∵PE=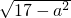
，PF=
∴
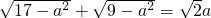
∴化简可得3a4-26a2+16=0
∴a2=8或a2=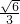
（舍去）
∴a=2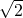
∴2a=4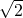
故选A．
点评：本题考查空间距离的计算，考查学生分析解决问题的能力，属于中档题．
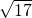，PC=PD=3，则该四面体的棱长是A.4
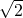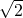B.2C.4D.8在线课程A分析：取AB，CD的中点E，F，则EF⊥AB，EF⊥CD，且P在EF上，设出棱长，建立方程，即可求得结论．
解答：
解：取AB，CD的中点E，F，则EF⊥AB，EF⊥CD，且P在EF上设四面体的棱长是2a，则EF=
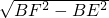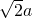
=∵PE=
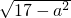，PF=∴
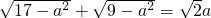
∴化简可得3a4-26a2+16=0
∴a2=8或a2=
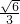（舍去）∴a=2
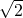
∴2a=4
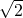
故选A．
点评：本题考查空间距离的计算，考查学生分析解决问题的能力，属于中档题．
