已知函数f+1.x∈R.的最小正周期,在区间上的最小值和最大值.
已知函数f(x)=2cosx(sinx-cosx)+1,x∈R.
(I)求函数f(x)的最小正周期;
(II)求函数f(x)在区间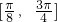 上的最小值和最大值.在线课程解:(I)f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=
上的最小值和最大值.在线课程解:(I)f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=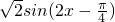 .
.
因此,函数f(x)的最小正周期为π.
(II)因为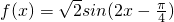 在区间
在区间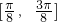 上为增函数,在区间
上为增函数,在区间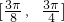 上为减函数,
上为减函数,
又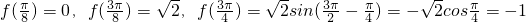 ,
,
故函数f(x)在区间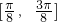 上的最大值为
上的最大值为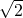 ,最小值为-1.
,最小值为-1.
分析:(I)先利用二倍角公式和两角和公式对函数解析式化简整理,然后利用正弦函数的性质求得函数的最小正周期.
(II)根据正弦函数的单调性和x的范围,进而求得函数的最大和最小值.
点评:本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数y=Asin(ωx+?)的性质等基础知识,考查基本运算能力.

(I)求函数f(x)的最小正周期;
(II)求函数f(x)在区间
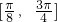 上的最小值和最大值.在线课程解:(I)f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=
上的最小值和最大值.在线课程解:(I)f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=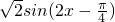 .
.因此,函数f(x)的最小正周期为π.
(II)因为
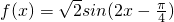 在区间
在区间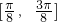 上为增函数,在区间
上为增函数,在区间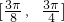 上为减函数,
上为减函数,又
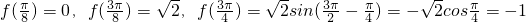 ,
,故函数f(x)在区间
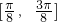 上的最大值为
上的最大值为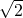 ,最小值为-1.
,最小值为-1.分析:(I)先利用二倍角公式和两角和公式对函数解析式化简整理,然后利用正弦函数的性质求得函数的最小正周期.
(II)根据正弦函数的单调性和x的范围,进而求得函数的最大和最小值.
点评:本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数y=Asin(ωx+?)的性质等基础知识,考查基本运算能力.



