四棱锥P-ABCD中.AD⊥面PAB.BC⊥面PAB.底面ABCD为梯形.AD=4.BC=8.AB=6.∠APD=∠CPB.满足上述条件的四棱锥的顶点P的轨迹是A.圆的一部分B.椭圆的一部分C.球的一
四棱锥P-ABCD中，AD⊥面PAB，BC⊥面PAB，底面ABCD为梯形，AD=4，BC=8，AB=6，∠APD=∠CPB，满足上述条件的四棱锥的顶点P的轨迹是
A.圆的一部分B.椭圆的一部分C.球的一部分D.抛物线的一部分在线课程A
分析：以AB所在直线为x轴，AB的中垂线为y轴，建立平面直角坐标系，写出点A，B的坐标，根据条件得出Rt△APD∽Rt△CPB，
进而得出 APBP=ADBC=48=12，设出点P的坐标，利用两点间的距离公式，代入上式化简，根据轨迹方程，即可得到结论．
解答：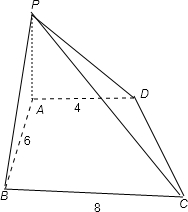
解：在平面PAB内，
以AB所在直线为x轴，AB的中垂线为y轴，建立平面直角坐标系．
设点P（x，y），则由题意可得 A（-3，0），B（3，0）．
∵AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，
∴Rt△APD∽Rt△CPB，
∴
．
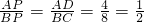即 BP2=4AP2，故有（x-3）2+y2=4[（x+3）2+y2]，
整理得：（x+5）2+y2=16，表示一个圆．
由于点P不能在直线AB上（否则，不能构成四棱锥），
故点P的轨迹是圆的一部分，
故选A．
点评：本题考查点轨迹方程的求法，以立体几何为载体考查轨迹问题，综合性强，考查了学生灵活应用知识分析解决问题的能力和知识方法的迁移能力，同时考查了运算能力，属于难题．
A.圆的一部分B.椭圆的一部分C.球的一部分D.抛物线的一部分在线课程A
分析：以AB所在直线为x轴，AB的中垂线为y轴，建立平面直角坐标系，写出点A，B的坐标，根据条件得出Rt△APD∽Rt△CPB，
进而得出 APBP=ADBC=48=12，设出点P的坐标，利用两点间的距离公式，代入上式化简，根据轨迹方程，即可得到结论．
解答：
解：在平面PAB内，以AB所在直线为x轴，AB的中垂线为y轴，建立平面直角坐标系．
设点P（x，y），则由题意可得 A（-3，0），B（3，0）．
∵AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，
∴Rt△APD∽Rt△CPB，
∴
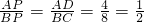．即 BP2=4AP2，故有（x-3）2+y2=4[（x+3）2+y2]，
整理得：（x+5）2+y2=16，表示一个圆．
由于点P不能在直线AB上（否则，不能构成四棱锥），
故点P的轨迹是圆的一部分，
故选A．
点评：本题考查点轨迹方程的求法，以立体几何为载体考查轨迹问题，综合性强，考查了学生灵活应用知识分析解决问题的能力和知识方法的迁移能力，同时考查了运算能力，属于难题．
