数列{an}中.a1=1.Sn是{an}的前n项和.且Sn+1=Sn+n.n∈N*.(Ⅰ)求数列{an}的通项公式,(Ⅱ)若.求数列{bn}的通项公式,(III)若.求数列{cn}的前n项和Tn.
数列{an}中,a1=1,Sn是{an}的前n项和,且Sn+1=Sn+n,n∈N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若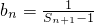 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(III)若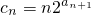 ,求数列{cn}的前n项和Tn.在线课程解:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n
,求数列{cn}的前n项和Tn.在线课程解:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n
所以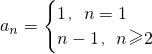 ,(3分)
,(3分)
(Ⅱ)由S1=a1=1,Sn+1=Sn+n,利用叠加法得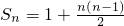 (6分)
(6分)
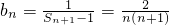 (8分)
(8分)
(III)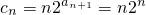 (9分)
(9分)
Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n①
2Tn=,1×22+2×23++(n-2)•2n-2+(n-1)•2n+n•2n+1②
①-②得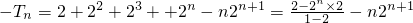 Tn
Tn
=(n-1)•2n+1+2.(14分)
分析:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n,由此能求出数列{bn}的通项公式.
(Ⅱ)由S1=a1=1,Sn+1=Sn+n,利用叠加法得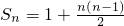 ,由此得到数列{bn}的通项公式.
,由此得到数列{bn}的通项公式.
(III)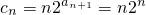 ,Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n,再由错位相减求和法能得到数列{cn}的前n项和Tn.
,Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n,再由错位相减求和法能得到数列{cn}的前n项和Tn.
点评:本题考查数列的性质和应用,解题时要认真审题,注意通项公式的求法和裂项求和法的运用.

(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若
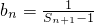 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;(III)若
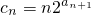 ,求数列{cn}的前n项和Tn.在线课程解:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n
,求数列{cn}的前n项和Tn.在线课程解:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n所以
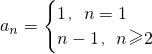 ,(3分)
,(3分)(Ⅱ)由S1=a1=1,Sn+1=Sn+n,利用叠加法得
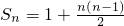 (6分)
(6分)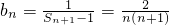 (8分)
(8分)(III)
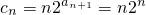 (9分)
(9分)Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n①
2Tn=,1×22+2×23++(n-2)•2n-2+(n-1)•2n+n•2n+1②
①-②得
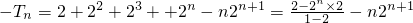 Tn
Tn=(n-1)•2n+1+2.(14分)
分析:(Ⅰ)由Sn+1=Sn+n,n∈N*得an+1=Sn+1-Sn=n,由此能求出数列{bn}的通项公式.
(Ⅱ)由S1=a1=1,Sn+1=Sn+n,利用叠加法得
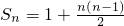 ,由此得到数列{bn}的通项公式.
,由此得到数列{bn}的通项公式.(III)
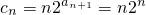 ,Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n,再由错位相减求和法能得到数列{cn}的前n项和Tn.
,Tn=1×2+2×22+3×23++(n-1)•2n-1+n•2n,再由错位相减求和法能得到数列{cn}的前n项和Tn.点评:本题考查数列的性质和应用,解题时要认真审题,注意通项公式的求法和裂项求和法的运用.



