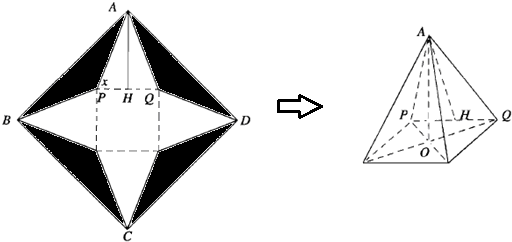
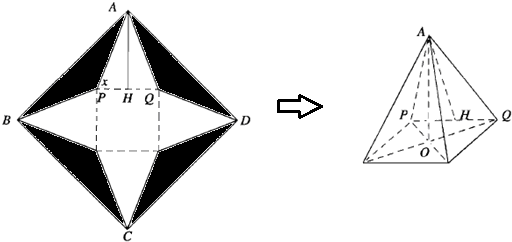
如图:设一正方形ABCD边长为2分米.切去阴影部分所示的四个全等的等腰三角形.剩余为一个正方形和四个全等的等腰三角形.沿虚线折起.使A.B.C.D四点重合.记为A点.恰好能做成一个正四棱锥.图中AH⊥
如图:设一正方形ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,使A、B、C、D四点重合,记为A点.恰好能做成一个正四棱锥(粘贴损耗不计),图中AH⊥PQ,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
 在线课程解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
在线课程解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
∵正方形ABCD边长为2分米,∴AH=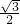 a=
a=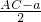 =
=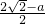 ,解得a=
,解得a=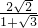 =
=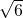 -
-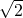
∴正四棱锥的棱长a=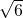 -
-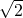
∴PO=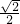 a,AO=
a,AO=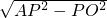 =
=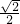 a,
a,
∴V=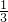 ×a2×AO=
×a2×AO=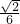 a3=
a3=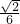 ×(
×(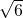 -
-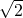 )3=4
)3=4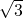 -
-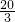
(II)∵AH= PQ×tanx=
PQ×tanx=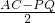 =
=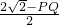 =
=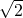 -
- PQ
PQ
∴PQ=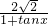 ,AH=
,AH=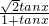
∴S=4× ×PQ×AH
×PQ×AH
=2×PQ×AH
=2×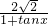 ×
×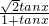
=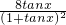 x∈[
x∈[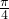 ,
,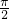 )
)
∵S=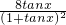 =
=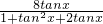 =
=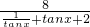 ≤
≤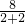 =2 (当且仅当tanx=1即x=
=2 (当且仅当tanx=1即x=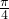 时取等号)
时取等号)
而tanx>0,故s>0
∴S的范围为(0,2]
分析:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,由此先计算出此正四棱锥的棱长,再利用正棱锥的性质计算其体积即可;
(II)先利用等腰三角形APQ的底角为x的特点,将侧棱长和底边长分别表示为x的函数,再利用棱锥的体积计算公式将棱锥体积表示为关于x的函数,最后可利用均值定理求函数的值域
点评:本题主要考查了正四棱锥的几何性质,正四棱锥中的棱长、高、体积的计算,建立函数模型并求其最值的方法,有一定的难度

(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
 在线课程解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
在线课程解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,∵正方形ABCD边长为2分米,∴AH=
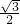 a=
a=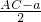 =
=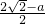 ,解得a=
,解得a=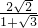 =
=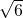 -
-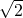
∴正四棱锥的棱长a=
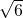 -
-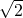
∴PO=
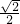 a,AO=
a,AO=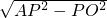 =
=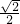 a,
a,∴V=
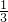 ×a2×AO=
×a2×AO=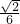 a3=
a3=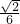 ×(
×(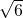 -
-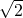 )3=4
)3=4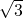 -
-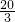

(II)∵AH=
 PQ×tanx=
PQ×tanx=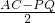 =
=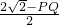 =
=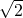 -
- PQ
PQ∴PQ=
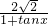 ,AH=
,AH=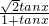
∴S=4×
 ×PQ×AH
×PQ×AH=2×PQ×AH
=2×
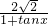 ×
×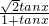
=
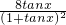 x∈[
x∈[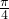 ,
,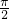 )
)∵S=
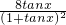 =
=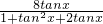 =
=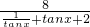 ≤
≤ =2 (当且仅当tanx=1即x=
=2 (当且仅当tanx=1即x=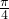 时取等号)
时取等号)而tanx>0,故s>0
∴S的范围为(0,2]
分析:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,由此先计算出此正四棱锥的棱长,再利用正棱锥的性质计算其体积即可;
(II)先利用等腰三角形APQ的底角为x的特点,将侧棱长和底边长分别表示为x的函数,再利用棱锥的体积计算公式将棱锥体积表示为关于x的函数,最后可利用均值定理求函数的值域
点评:本题主要考查了正四棱锥的几何性质,正四棱锥中的棱长、高、体积的计算,建立函数模型并求其最值的方法,有一定的难度



