已知向量.(1)求, (2)求与的夹角的余弦值,(3)求向量的坐标 (4)求x的值使与为平行向量.
已知向量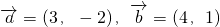 ,
,
(1)求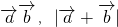 ; (2)求
; (2)求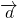 与
与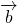 的夹角的余弦值;
的夹角的余弦值;
(3)求向量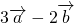 的坐标 (4)求x的值使
的坐标 (4)求x的值使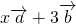 与
与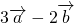 为平行向量.在线课程解:(1)
为平行向量.在线课程解:(1)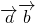 =(3,-2)•(4,1)=3×4+(-2)×1=10,
=(3,-2)•(4,1)=3×4+(-2)×1=10,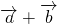 =(3,-2)+(4,1)=(7,-1),
=(3,-2)+(4,1)=(7,-1),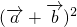 =50,∴
=50,∴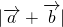 =
=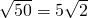
(2)设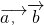 夹角为θ,则cosθ=
夹角为θ,则cosθ=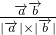 =
=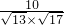 =
=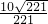
(3)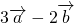 =(9,-6)-(8,2)=(1,-8)
=(9,-6)-(8,2)=(1,-8)
(4)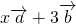 =(3x,-2x)+(12,3)=(3x+12,-2x+3),
=(3x,-2x)+(12,3)=(3x+12,-2x+3),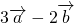 =(1,-8),由已知得,-2x+3=-8(3x+12),整理并解得x=
=(1,-8),由已知得,-2x+3=-8(3x+12),整理并解得x=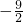
分析:(1)两个向量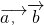 的数量积等于它们对应坐标的乘积的和;向量的模等于自身数量积再开方,先求
的数量积等于它们对应坐标的乘积的和;向量的模等于自身数量积再开方,先求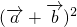 再开方
再开方
(2)根据向量数量积计算公式的变形,求出两向量夹角的余弦值.
(3)实数与向量的积的坐标等于用实数乘以原来向量的相应坐标.两个向量的差的坐标等于它们对应坐标的差.
(4)根据平面向量的坐标表示,列出关于x的方程并解即得.
点评:本题考查向量的数量积,模,夹角.向量共线的条件判断.属于常规题目.

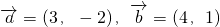 ,
,(1)求
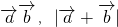 ; (2)求
; (2)求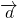 与
与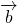 的夹角的余弦值;
的夹角的余弦值;(3)求向量
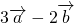 的坐标 (4)求x的值使
的坐标 (4)求x的值使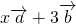 与
与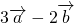 为平行向量.在线课程解:(1)
为平行向量.在线课程解:(1)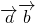 =(3,-2)•(4,1)=3×4+(-2)×1=10,
=(3,-2)•(4,1)=3×4+(-2)×1=10,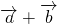 =(3,-2)+(4,1)=(7,-1),
=(3,-2)+(4,1)=(7,-1),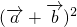 =50,∴
=50,∴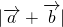 =
=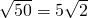
(2)设
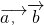 夹角为θ,则cosθ=
夹角为θ,则cosθ=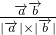 =
=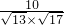 =
=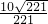
(3)
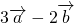 =(9,-6)-(8,2)=(1,-8)
=(9,-6)-(8,2)=(1,-8)(4)
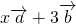 =(3x,-2x)+(12,3)=(3x+12,-2x+3),
=(3x,-2x)+(12,3)=(3x+12,-2x+3),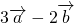 =(1,-8),由已知得,-2x+3=-8(3x+12),整理并解得x=
=(1,-8),由已知得,-2x+3=-8(3x+12),整理并解得x=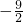
分析:(1)两个向量
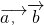 的数量积等于它们对应坐标的乘积的和;向量的模等于自身数量积再开方,先求
的数量积等于它们对应坐标的乘积的和;向量的模等于自身数量积再开方,先求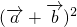 再开方
再开方(2)根据向量数量积计算公式的变形,求出两向量夹角的余弦值.
(3)实数与向量的积的坐标等于用实数乘以原来向量的相应坐标.两个向量的差的坐标等于它们对应坐标的差.
(4)根据平面向量的坐标表示,列出关于x的方程并解即得.
点评:本题考查向量的数量积,模,夹角.向量共线的条件判断.属于常规题目.



